Nah, pada postingan kali ini saya akan membahas cara penentuan luas daerah menggunakan defenisi integral tentu atau integral Riemann.
Perhatikan gambar berikut :
Kita akan menentukan luas daerah yang di arsir pada grafik diatas.
Pada interval [0,2] kita akan membagi menjadi sub-interval dengan lebar yang sama, misal kita akan membagi luas daerah yang di arsir tersebut menjadi empat bagian, maka :
Dengan demikian kita akan menggambar persegi panjang pada gambar yang diarsir tersebut dengan masing-masing 1,5 satuan lebar dan tingginya diambil dari titik ujung persegi panjang sebelah kanan :
Mari tentukan luasnya berdasarkan gambar di atas. Pertama, lebar tiap persegi panjang adalah 1,5 dan kemudian tingginya di ambil dari nilai fungsi titik ujung persegi panjang sebelah kanan. Sehingga perkiraan luasnya adalah :
diperoleh jika penghitungan berdasarkan titik ujung persegi panjang sebelah kanan luas daerahnya adalah 5,75 satuan luas.
Lalu, bagaimana jika penentuan luas daerah berdasarkan titik ujung persegi panjang sebelah kiri?Oke, perhatikan gambar berikut :
Sehingga perkiraan luas daerah tersebut adalah :
Bisa kita lihar perbedaan perkiraan luas di antara keduanya. Karena dengan penentuan luas daerah berdasarkan titik ujung persegi panjang sebelah kiri adanya ruang kosong yang bisa kita lihat di bawah grafik.
Lalu, ada satu lagi cara yang di rasa akurat yaitu penentuan tinggi persegi panjang yang kita gambar berdasarkan titik tengah.
Perhatikan gambar berikut :
Maka, perkiraan luas daerah tersebut adalah :
Kita sekarang memperoleh tiga perkiraan luas yang berbeda. Maka perkiraan luas yang mendekati keakuratan adalah :
Dapat kita lihat perkiraan luas menggunakan aturan titik tengah lebih mendekati keakuratan daripada dua cara yang lain.
Lalu, bagaimana jika persegi panjang yang kita gambar untuk menaksir luas daerah yang di arsir tersebut kita perbanyak?
Misal kita akan menggambar delapan buah persegi panjang. Perhatikan masing-masing gambar berikut :
Dengan pendekatatan tinggi persegi panjang berdasarkan titik ujung sebelah kanan :
Perkiraan luas daerahnya adalah :
Dengan pendekatan tinggi persegi panjang berdasarkan titik ujung sebelah kiri :
Perkiraan luas daerahnya adalah :
Terakhir, dengan pendekatan tinggi persegi panjang berdasarkan titik tengah :
Perkiraan luas daerahnya adalah :
Dapat kita lihat, memperbanyak jumlah persegi panjang yang kita gunakan untuk menghitung luas daerah pada grafik tersebut, maka akan lebih mengakuratkan perkiraan luas daerah yang kita peroleh.
Sekarang, mari kita jabarkan rumus umumnya.
Misalkan y=f(x) adalah kurva kontinu dengan interval [a,b]
Dan kita akan menggambar persegi panjang sebanyak n buah, maka lebar tiap-tiap interval adalah :
Sehingga grafiknya menjadi :
Sehingga luas total daerah yang di arsir adalah luas total seluruh persegi panjang :
Apabila menggunakan notasi sigma persamaan di atas dapat ditulis menjadi :
Bentuk tersebut di kenal dengan jumlah Riemann.
Seperti yang sudah dijelaskan di atas, apabila subinterval (n) semakin banyak maka perkiraan luasnya semakin akurat. Jika n mendekati tidak terhingga maka luasnya semakin tepat. Dengan demikian luas daerah ditentukan dengan :
Bentik di atas dapat disederhanakan menggunakan notasi integral:yang dinamakan sebagai integral tentu atau integral Riemann.






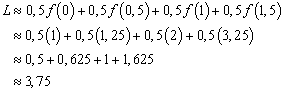

















Tidak ada komentar:
Posting Komentar