Maka, luas daerah yang diarsir adalah :
Atau agar lebih mudah mengingat rumusnya :
Contoh :
Rumuskan luas-luas daerah yang diraster pada gambar berikut dengan menggunakan integral tentu, kemudian hitunglah luas-luas daerah itu .
Penyelesaian :
Untuk menghitung luas daerah pada gambar di atas dapat dilakukan dengan dua cara.
Cara I :
Bagi kedua luas wilayah yang di arsir pada
gambar tersebut
Jadi, luas daerah gambar tersebut adalah : 9/2 satuan luas
Cara II :
Maka pengintegralannya :
Oke, pembahasan lebih lengkap bisa di lihat atau di download pada link berikut INI.













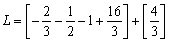







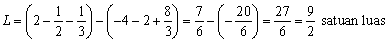
Tidak ada komentar:
Posting Komentar